Find Asymptotes Of Secant Function
Ray is a licensed engineer in the Philippines. He loves to write about mathematics and ceremonious engineering.
Secant is an even function that serves as the reciprocal of the cosine function. It is a trigonometric function with a more extensive graph in the negative direction rather than a smaller ane. As the fractions in the cosine function become smaller or closer to goose egg, their reciprocals in the secant function get broader and longer in the opposite management.
A secant function has the same menstruation as its reciprocal. The cosine part has a period of 2π, so the secant function has a catamenia of 2π. It is discontinuous at values for x, for which its reciprocal is zippo. For secant functions, say y = sec (x), the values for which the function is not defined are 10 = ± [(2n +i)π] / two and the asymptotes are at ten = ± [(2n +1)π] / ii. Near those values of x for which each function is insignificant, the values of the trigonometric functions are unbounded. Hence, the aamplitude is insignificant for these functions.
The graph of a secant tin can be sketched by first sketching the graph of y = cos (x) and then estimating the reciprocal of cos (ten). Take a look at the y = sec (x) and y = cos (x) shown below. As observed, the u-shapes of the secant graph impact the graph of cos (x) at maximum and minimum points.

Secant Graph and Cosine Graph. The U-shapes of the secant graph are tangent to its reciprocal function, cosine. The blue curve is y = cos (ten) and the blackness curve is y = sec (x), which is the reciprocal of cos (x).
Secant Graph Properties
For the secant function y = α sec βx,
- Period. The menses is the absolute value of |2π / β|. For y = sec (x), the period is 2π.
- Amplitude. Secant functions have no divers amplitude. The secant graphs go on unending or space in vertical directions. However, for some cases, given the equation y = α sec (βx - c) - d, the secant graph will have an amplitude of |α|. It ways that 1 should multiply all points of the vertical axis (y-coordinates) in the graph past the value of α. However, however, the graph goes on forever in the vertical direction.
- Domain. The domain of y = sec (ten) is all real numbers 10, except ten = ± [(2n +1)π] / 2. In other words, the domain of the secant role excludes π/2 + knorth, where chiliad is applicable for all integers. Ordered pairs of the form (x, sec (x)) make up the secant function. Since sec (10) is the reciprocal of cos (x), the domain of the secant office is the set of real numbers, except those for which cos (ten) = 0. Hence, the domain contains all elements x ∈ ℝ such that: x ≠ π/2 + nπ satisfies. Since |cos ten| < 1 for all s ∈ ℝ, its reciprocal satisfies |sec 10| > 1, which determines the range of the secant function.
- Range. The range of y = sec (x) is all real numbers y, except -1 < y < ane. The range of y = sec (10) is equal to (-∞, -1] U [1, ∞).
- Continuity. The function y = sec (x) is discontinuous at x = ± [(2n +one)π] / ii.
- Vertical Asymptotes. The vertical asymptotes of y = sec (x) occur at π/2 and repeat every π units. The x-intercepts of y = cos (x) are the asymptotes for y = sec (x). The vertical asymptotes of y = sec (x) is given past the equation x = π/2 + πn. In other resources, information technology is like shooting fish in a barrel to identify the vertical asymptotes for the secant graph past solving the inequality -π/2 < βx + c < π/two.
- Maximum and Minimum Values. The maximum values of y = cos (ten) are minimum values of y = sec(x). On the other hand, the minimum values of y = cos (10) are the maximum values of the negative sections of y = sec (10).
- X-intercepts. The trig secant graph has no ten-intercepts.
- Symmetry. Secant graphs are ever symmetrical about the y-axis.
Annotation: For the secant function with more terms, utilise phase shifting. Say, y = α sec (βx - c) - d, the flow of the function is still 2π / β, the phase shift/horizontal shift is c/β, and the vertical shift is -d.
How to Graph a Secant Function
In cartoon the secant curve on graphing newspaper, accept note that secant graphs with no shifts automatically have x and y coordinates equal to (0,1), (1,-1), and (two,ane). However, in that location are few things needed to consider for cases with variations to draw the secant graph fully. Just follow the steps shown below.
- Identify the menstruation of the given secant equation. As mentioned before, the period of any secant function is 2π / β, given an equation y = α sec (βx - c) - d. Therefore, the period of the secant graph 2π / β is the length of one cycle of the secant bend.
- Locate the asymptotes and other parameters of the secant graph. Since secant is the reciprocal of the cosine role, any point on the cosine graph where the value is nil generates a vertical asymptote on the secant graph. Information technology is helpful since it defines the secant graph early. Take note that the parent graph y = cos (x) has 0 values at angles 3π/2 and π/two.
- Place if there are horizontal and vertical shifts. For y = α sec (βx - c) - d, the horizontal shift is c/β to the right, and the vertical shift is -d in the down direction.
- Identify the aamplitude. The aamplitude of the secant equation y = α sec (βx - c) - d equals |α|. Multiply all values or points with |α|.
- Tabulate values of the cosine and secant functions. Apply this stride if values along the curves of the secant graph are needed. Substitute the radians into the given equation, of course, excluding the asymptotes obtained from the outset step.
To be able to graph a secant function, see the examples given below.
Instance 1: Sketching the Secant Graph With Horizontal Shift
Sketch the graph of the secant equation y = sec (10 - π/4).
Solution
First, identify the parameters before sketching the trigonometric secant graph.
Range: Place the range of the given secant equation.
Range: (-∞, -1) U (1, +∞)
Scroll to Go along
Read More From Owlcation
Menstruation: Solve for the period of y = sec (2x - π/3) using the formula p = 2π/β. Since the resulting period is π, this means that the secant graph is
2π/β = 2π/2
2π/2 = π
Horizontal Shifts: Since the term -π/4 is present in the equation, so the secant graph shifts horizontally. Information technology means that the graph volition move horizontally to the right direction π/4 units.
y = sec (x - π/4)
Horizontal shift = - π/4
Vertical Shifts: None
Vertical Asymptotes: Solve for the vertical asymptotes of the equation using the given inequality beneath.
-π/ii < 10 - π/4 < π/2
x - π/4 < π/ii
x < π/2 + π/4
x < 3π/4
-π/2 < 10 - π/four
-π/2 + π/4 < x
-π/4 < x
Finally, sketch the graph by locating the vertical asymptotes, the horizontal shift, and the menstruum. Besides, bank check the tabulated values of the given function to locate specific points as shown in the table shown.
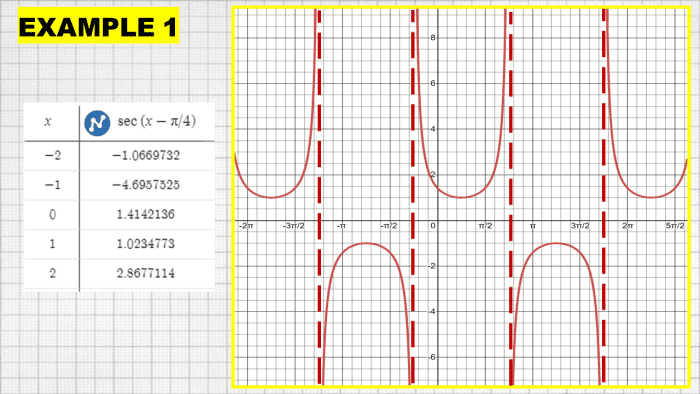
Secant Graph With Horizontal Shift
Example ii: Secant Graph With Amplitude
Sketch the graph of the secant equation y = two sec (x - π/four).
Solution
Start, identify the parameters before sketching the trigonometric secant graph.
Range: Identify the range of the given secant equation.
Range: (-∞, -ane) U (1, +∞)
Period: Solve for the period of y = sec (2x - π/3) using the formula p = 2π/β. Since the resulting menstruation is π, this means that the secant graph is
2π/β = 2π/2
2π/1 = π
Horizontal Shifts: Since the term -π/4 is present in the equation, then the secant graph shifts horizontally. Information technology means that the graph will motion horizontally to the right direction π/4 units.
y = sec (x - π/4)
Horizontal shift = - π/4
Vertical Shifts: None
Vertical Asymptotes: Solve for the vertical asymptotes of the equation using the given inequality beneath.
-π/ii < x - π/4 < π/two
x - π/4 < π/ii
10 < π/2 + π/4
x < 3π/4
-π/ii < x - π/4
-π/two + π/four < x
-π/4 < x
Amplitude: Multiply the y-coordinates of the graph to execute the amplitude of the secant graph.
Finally, sketch the graph by locating the vertical asymptotes, the horizontal shift, and the menstruation.
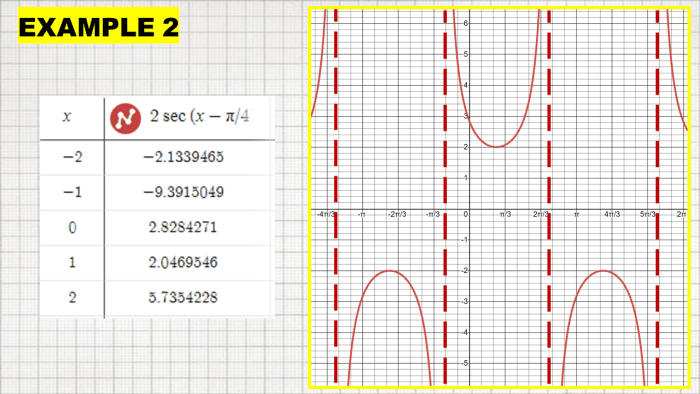
Secant Graph With Amplitude
Case 3: Secant Graph With Vertical Shift
Identify the parameters of the secant equation y = sec (ten) - 3 and sketch it.
Solution
Identify the parameters before sketching the graph of the secant office.
Range: Identify the range of the given secant equation.
Range: (-∞, -1) U (i, +∞)
Period: Solve for the flow of y = sec (x) - iii using the formula p = 2π/β. Since the resulting menstruation is π, this means that the secant graph is
2π/β = 2π/one
2π/1 = 2π
Vertical Shifts: In that location is a vertical shift of iii units downwardly since it is a negative shift.
Vertical Asymptotes: The vertical asymptotes of the equation using the inequality formula is -π/2 < x < π/2. It means that the unique feature about this secant graph is its vertical shift and no adjustments for its vertical asymptotes.
Lastly, sketch the graph past locating the vertical asymptotes, the vertical shift, and the menses. Please see the tabulated values for reference.
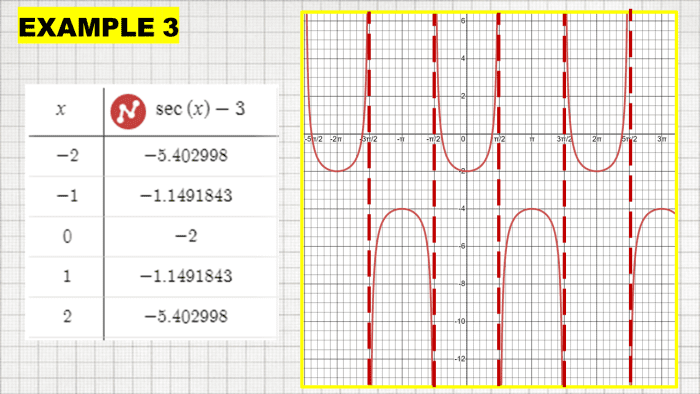
Secant Graph With Vertical Shift
Instance 4: Secant Graph With Horizontal and Vertical Shifts
Sketch the graph y = sec (x - 2) + 3.
Solution
Menstruum: Solve for the period of y = sec (x -ii) + three using the formula p = 2π/β.
2π/β = 2π/1
2π/β = 2π
Horizontal Shifts: Since the term -2 is present in the equation, and so the secant graph shifts horizontally. It means that the graph will move horizontally to the correct direction two units.
y = α sec (βx - c)
Horizontal shift = c/β
Horizontal shift = - 2/1
Horizontal shift = - ii
Vertical Shifts: There is a vertical shift of 3 units upward since it is a positive move.
Vertical Asymptotes: Solve for the vertical asymptotes of the given equation using the given below.
-π/2 < 10 - 2 < π/2
10 - two < π/2
ten < π/two + two
-π/2 < ten - 2
2 - π/2 < ten
Lastly, sketch the graph by locating the vertical asymptotes, horizontal and vertical shifts, and the flow. Please see the tabulated values for reference.
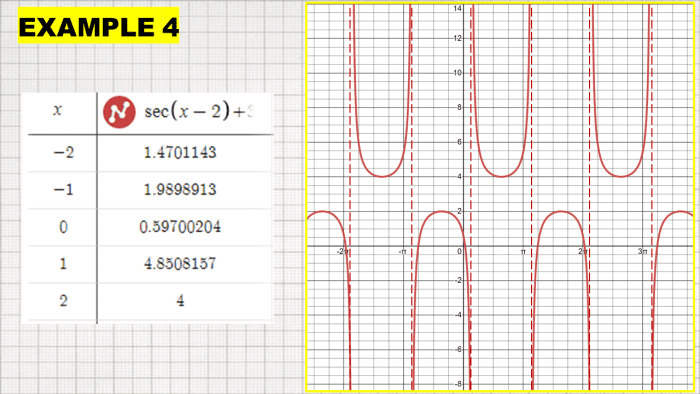
Secant Graph With Horizontal and Vertical Shifts
Example 5: Sketching a Secant Graph With Horizontal Shift
Sketch the graph of y = sec (2x - π/3).
Solution
Identify all parameters in sketching the graph of the given secant role.
Range: Commencement is to identify all the parameters needed in graphing the given secant office. Place the range of the given secant equation.
Range: (-∞, -1) U (1, +∞)
Period: Solve for the catamenia of y = sec (2x - π/three) using the formula p = 2π/β.
2π/β = 2π/2 = π
Horizontal Shifts: Since the term -π/three is present in the equation, then the secant graph shifts horizontally. Nevertheless, first, rewrite the equation eliminating the coefficient of the variable x. It means that the graph will move horizontally to the correct direction π/6 units.
y = α sec (βx - c)
Horizontal shift = c/β
y = sec (2x - π/3)
y = sec [2 (x - π/half-dozen)]
Horizontal shift = - π/half-dozen
Vertical Asymptotes: Solve for the vertical asymptotes of the given equation using the given below.
2x - π/3 = π/2 + kπ
2x = π/2 + π/3 + kπ
2x = 5π/half-dozen + kπ
x = 5π/12 + kπ/2
At g = 0
ten = 5π/12 + (0)π/ii
10 = 5π/12
Finally, sketch the secant function y = sec (2x - π/3). Start with π/half-dozen units to the right and ends at 7π/6, which is π/6 + π.

Sketching a Secant Graph With Horizontal Shift
Explore More than Articles Almost Graphs
- How to Graph an Ellipse Given an Equation
Larn how to graph an ellipse given the general grade and standard class. Know the different elements, properties, and formulas necessary in solving problems about ellipse. - How to Graph a Circle Given a General or Standard Equation
Learn how to graph a circle given the general form and standard grade. Familiarize with converting general grade to standard form equation of a circle and know the formulas necessary in solving issues about circles.
This content is accurate and true to the best of the writer'due south cognition and is not meant to substitute for formal and individualized advice from a qualified professional.
© 2021 Ray
Find Asymptotes Of Secant Function,
Source: https://owlcation.com/stem/Secant-Graph-How-to-Graph-a-Secant-Function
Posted by: marcellosalict67.blogspot.com


0 Response to "Find Asymptotes Of Secant Function"
Post a Comment